Hypergeometric 超幾何分布

Hypergeometric Distribution 中文稱作「超幾何分布」，為離散型分布。其係描述：假設從有限數量的母體，其大小為 Ｍ，其中包含特定性值 Ｎ 件與不符合的特定性值 (M-N) 件，以取後不放回（without replacement；WOR）的方式，抽出 n 件，其中符合特定性質的樣本為 ｋ 件的機率。把以上情境表示為：若隨機變數 X 服從 Hypergeometric (M, n, N)，則其 PMF 可表示為

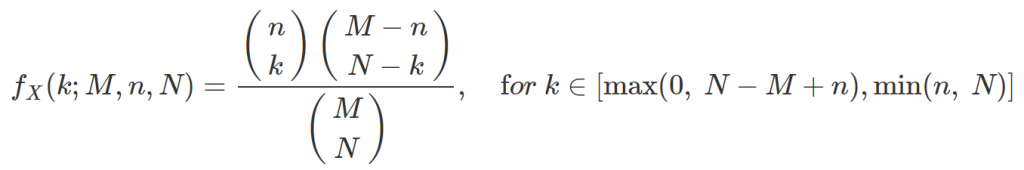
另外，順便提到，函數為 PDF 或 PMF 的條件。

若一函數 $f_X(x)$ 為隨機變數 $X$ 之 PDF 或 PMF，若且唯若滿足以下條件：

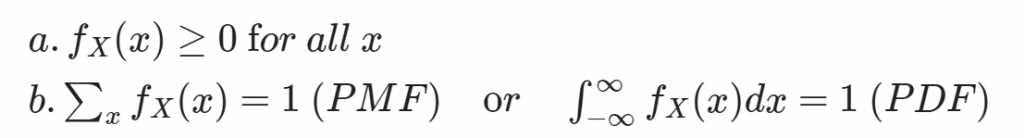
-- Statistical Inference，George Casella and Roger L. Berger，36-37頁。

a.代表在代入樣本點時函數值係非負；b. 代表函數加總所有樣本點之值為 1。讀者不妨嘗試證明上式 Hypergeometric 分配函數為 PMF。清楚記得之前筆者就讀大學時，機率課的期中考有一題就是要求證明此函數為 PMF。如果能夠依靠自己證明這題，代表你也很熟悉二項式係數了！

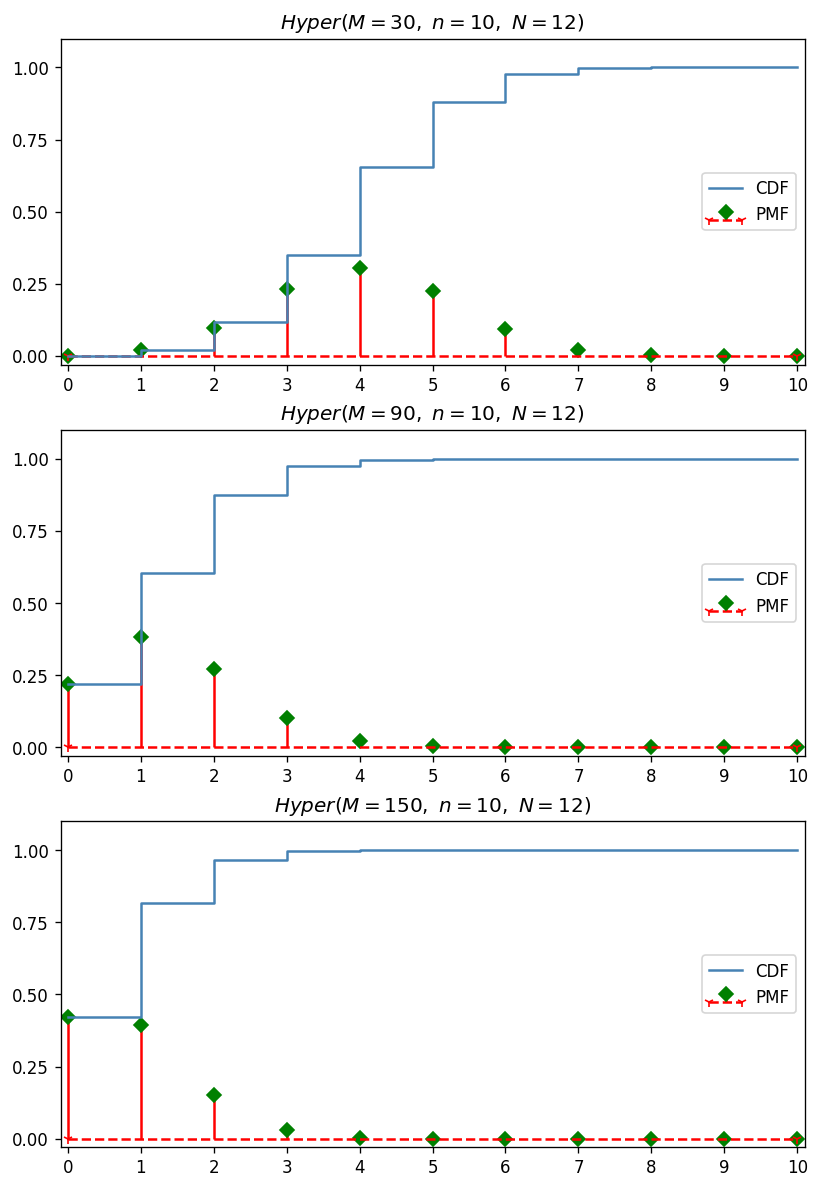
回到原題，下圖為固定符合特定條件的母體數 N 與抽出的筆數 n ，在設置不同的母體數 M 之下，Hypergeometric 分配的 PMF 與 CDF。可以觀察到隨 M 增加，PMF 顯著大於 0 的範圍越小，X 的離散程度越小；同時依據圖中的 CDF，可看出 PMF 值的和隨 M 增加也越快累積到 1。由下圖也可看出 Hypergeometric 的分布函數符合函數為 PMF 的條件。

在 Python 的 PMF 程式碼為 hypergeom.pdf ，其程式所使用的 PMF 如上式。在使用此程式碼時，需特別注意其複雜的參數 $(M, n, N)$ 與變數 $k$，例如：擺放之順序、數值大小等，尤其是在取樣時，很容易不小心就放錯變數。

Hypergeometric 分配的 PMF 與 CDF 的 Python 程式碼如下，其中程式使用 ax[i].set_ylim(0-0.1, 1.1) 與 ax[i].set_xbound(0-0.1, n+0.1) 調整個子圖的視窗範圍，使 PMF 與 CDF 的頭尾可以全然呈現，而不會被切割。其中 ax[i].set_xbound(*) 的功能類似於 ax[i].set_xlim(*)，前者在設定特定的範圍後，會依據實際情況自動調整畫圖範圍；而後者不會，以當初設定的上、下限範圍畫圖，詳情可參考：What is the difference between set_xlim and set_xbound?。

# Hypergeometric distribution

from scipy.stats import hypergeom

fig, ax = plt.subplots(3, 1, figsize=[8, 12], dpi=120)

M = np.linspace(30, 150, 3, dtype='int')
n = 10
N = 12


x = np.arange(n + 1)

for i in range(len(M)):
  # PMF
  y = hypergeom.pmf(x, M[i], n, N)
  ax[i].stem(y, linefmt='r-', markerfmt='gD', basefmt='r1--')
  # CDF
  Y = hypergeom.cdf(x, M[i], n, N)
  ax[i].plot(Y, drawstyle='steps-post', color='steelblue')

  ax[i].set_xticks(np.arange(0, n+1, 1))
  ax[i].set_title(r'$Hyper (M={},\ n={},\ N={})$'.format(M[i], n, N))
  ax[i].set_yticks(np.arange(0, 1+0.25, 0.25))
  ax[i].set_ylim(0-0.03, 1+0.1)
  ax[i].set_xbound(0-0.1, n+0.1) # 功能似 set_xlim，但可自動調整範圍

plt.show()